Algorithm

HackerRank/Algorithm/Dynamic Programming/Angry Children 2

Problem Summary

Suppose there are K packets with (x1, x2, x3,….xk) candies in them, where xi denotes the number of candies in the ith packet, then we define unfairness as

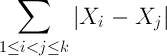
Unfairness

Given N packets, find the minimum unfairness when you pick K out of N packets.

Solution

Obviously, we only need to consider the cases that K packets with the “closest” values, so we sort the array first.

Then let f[i] be the unfairness when we choose x[i],x[i+1],…,x[i+K-1].

In order to reduce time complexity, we need to find out the recurrence relation between f[i] and f[i+1].

f[i] = |x[i+K-1] - x[i+K-2]| + |x[i+K-1] - x[i+K-3]| + … + |x[i+K-1] - x[i]|

      + |x[i+K-2] - x[i+K-3]| + |x[i+K-2] - x[i+K-4]| + … + |x[i+K-2] - x[i]|

      + …

      + |x[i+1] - x[i]|

So, f[i+1] = f[i] + (K-1) × (x[i+K] + x[i]) - 2 × (x[i+1] + x[i+2] + … + x[i+K-1]).

The answer is the minimum of f[i] (1 ≤ i ≤ N-K+1).

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <climits>
using namespace std;
const int maxn = 100002;
int n,m;
long long d[maxn],sum[maxn];
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%lld",&d[i]);
    sort(d+1,d+n+1);
    for(int i=1;i<=n;i++)
        sum[i]=sum[i-1]+d[i];
    long long cur,ans=0;
    for(int i=1;i<=m;i++)
        ans += d[i] * (long long)(i-1 - (m-i));
    cur = ans;
    for(int i=2;i<=n-m+1;i++)
    {
        cur += (d[i-1] + d[i+m-1]) * (long long)(m-1) - (sum[i+m-2]-sum[i-1])*2;
        if(cur<ans) ans=cur;
    }
    printf("%lld\n", ans);
    return 0;
}