Algorithm

LeetCode/Regions Cut by Slashes

Problem Summary

Given a N × N grid of 1 × 1 squares, each square consists of a ‘/‘, ‘\’, or blank space. Find the number of regions.

Solution

First, we split every square into two parts: the upper part and the lower part, and build a new graph.

As the following image shows, there are three cases:

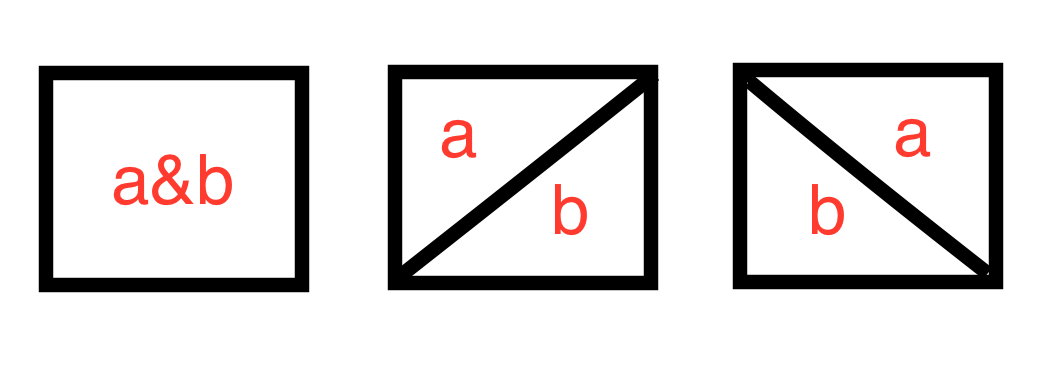
Square (i, j) is now two nodes a = (i × n + j) × 2 + 1 and b = a + 1.

If s[i][j] == ‘ ‘, then we connect a and b. Otherwise a and b shouldn’t be connected.
Then we need to connect square (i, j) with square (i + 1, j) and (i, j + 1).

  1. Between (i, j) and (i + 1, j) : we only need to connect b to the upper part of (i + 1, j), which is a + 2 × n.

  2. Between (i, j) and (i + 1, j) : we connect the right part of (i, j) and the left part of (i + 1, j).

After this, we can easily find the number of connected components of the new graph with union-find.

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class Solution {
public:
    vector<int> fa;
    
    int getfa(int x) {
        if (x == fa[x])
            return x;
        fa[x] = getfa(fa[x]);
        return fa[x];
    }
    
    void unify(int x, int y) {
        int a = getfa(x), b = getfa(y);
        if (a != b)
            fa[a] = b;
    }
    
    int regionsBySlashes(vector<string>& g) {
        int n = g.size();
        int tot = n * n * 2;
        
        fa = vector<int>(tot+1);
        for (int i = 1; i <= tot; ++i)
            fa[i] = i;
        
        for (int i = 0; i < n; ++i)
            for (int j = 0; j < n; ++j) {
                int a = (i*n + j) * 2 + 1;
                int b = a + 1;
                
                if (g[i][j] == ' ')
                    unify(a, b);
                
                if (j < n-1) {
                    int x = g[i][j] == '/' ? b : a;
                    int y = g[i][j+1] == '/' ? b+1 : b+2;
                    unify(x, y);
                }
                
                if (i < n-1)
                    unify(b, a + 2*n);
            }
        
        int ans = 0;
        for (int i = 1; i <= tot; ++i)
            if (fa[i] == i)
                ++ans;
        
        return ans;
    }
};